
This investigative project challenges students to research information about a number of sports and to engage in mathematical modelling. This activity is aimed at higher level GCSE and A Level students (Key Stage 4 and 5).
The Speed of the Game
Team games like football, hockey, rugby, basketball, handball and wheelchair rugby are played on pitches or courts of different sizes with different numbers of players. The density of players on the pitch plays a significant role in determining the nature of the game and how fast players need to react.
In this project activity you will investigate and compare the speed of the game in different sports. As is often the case when mathematicians use mathematics to understand the world, we need only simple calculations but we have to search out some of the pieces of information that we need and be able to make a simple estimate of the answer in order to get a good idea about whether it is worth doing a more detailed calculation.
Project
Suppose that the area of the pitch or court is A and there are N players (excluding goalkeepers) on the pitch at any one time. The number of players per unit area of pitch is
n = N/A
The average distance between players if they are randomly spread on the pitch is then
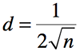
and so if they move at speed v to challenge other players what is the average time t between challenges?
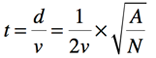
Plot graphs to show how t changes with the value of N for pitches of the sizes used for:
- football
- hockey
- rugby
- wheelchair rugby
- basketball
- handball
(You can think of other sports where this calculation would be relevant and investigate them too.) Assume the players move at 5 m/s.
Do you think these figures are realistic?
What other factors might influence how fast players need to react in different sports?
Background information
You can find useful information about Olympic and Paralympic sports including the size of the pitches and courts used on the London 2012 website.
These project ideas were originally developed by our Motivate project as follow-up activities to a talk by Professor John D Barrow FRS on 'The Maths Behind the Olympic Games'.

