-
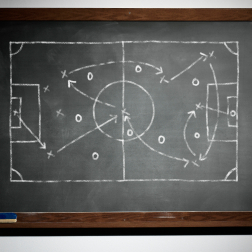
This activity follows on from Charting Success and encourages students to consider and analyse representations of data from the world of sport, to make sense of the stories they tell, and to analyse whether the right representation has been chosen for the purpose. It is aimed at secondary students (Key Stages 3 and 4).
-

Four sporty brainteasers in the context of fencing, hockey, football and international medal tables. This activity challenges students to be resourceful, to think logically and to work systematically, and is designed to be accessible to secondary maths students at Key Stages 3 and 4.
-

Decide which charts and graphs represent the number of goals two football teams scored in fifteen matches. This data handling activity is designed to get children talking meaningfully about mathematics, presenting and justifying arguments, and is aimed at primary school pupils at Key Stage 2.
-
What makes a perfect football? Anyone who plays or watches the game can tell you that the ball must be round, retain its shape, be bouncy but not too lively and, most importantly, be capable of impressive speeds. This last point is all down to the ball's surface, and Ken Bray explores how mathematics contributes to understanding this ultimate goal in ball design.
-
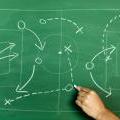
Sports statisticians, trainers and competitors create graphs, charts and diagrams to help them to analyse performance, inform training programmes or improve motivation. This activity encourages students to consider and analyse representations of data from a number of sports, and to discuss whether the right representation has been chosen for the purpose. It is aimed at secondary students (Key Stages 3 and 4).
-

The Olympic and Paralympic Games are a global celebration of excellence, determination and effort. Much of the media coverage, though, tends to focus on each country's tally of gold medals. This article by Rob Eastaway and John Haigh explores some of the mathematical questions raised by Olympic success. How well did Britain really do in 2008 in Beijing, with nineteen golds? Are some gold medals worth more than others? And are there even some sports the Olympics should drop?
-

How can mathematical models help us understand the beautiful game? Playing ball games often involves modifying the ball's flight to gain tactical advantage by hitting or kicking it in a particular way. Ken Bray investigates aerodynamics in football in this article, aimed at older students and the general public.
-

Team games like football, hockey, basketball, handball and wheelchair rugby are played on pitches or courts of different sizes with different numbers of players. The density of players on the pitch plays a significant role in determining the nature of the game and how fast players need to react. This investigative activity challenges students to research information about a number of sports and to engage in mathematical modelling, and is aimed at higher level GCSE and A Level students (Key Stage 4 and 5).
-

How should you decide which leg of the 4x400 metres relay the team's fastest runner should run? This short article, aimed at older students and the general public, looks at some of the tactical choices team captains and coaches face and how randomness might help.

